当我们夜晚失眠的时候，有一种传说中的通过诵念“1只羊，2只羊，…, 999只羊，…”这种数羊经文可以帮助我们入睡。当我们对一件事情表示惊叹或不满的时候，我们有时候会说有一万只羊驼在心中奔腾而过。这里面的“一种传说”、“1只羊”、“一件事”以及“一万只羊驼”都一种计数形式。

数字是我们平常能够接触的一种最抽象的编码，在我们这个星球上，几乎所有人都用以下的方式书写数字：

1 2 3 4 5 6 7 8 9 10

当我们看到数字：

3

我们可能会联想到 3 年高考与 5 年模拟，3 个苹果，3 只羊，或者 3 个别的什么东西。因为数字最开始产生时就很抽象，所以让我回到没有数字的时代，从新认识一下数字。这个问题就如下面苹果的数量：

3 apples

并一定要用符号“3”来表示，我们也可以用“11”或者“Ⅲ”表示。

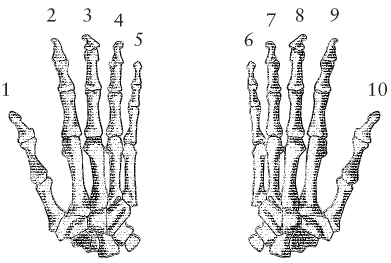
大多数历史学家认为数字最初起源于对事物的计数。最开始，人们用自己的手指来计数，这也说明了为什么大多数人类文明都是建立在以 10 为基的数字系统上的（有的时候是以5为基）。假如我们人类一只手的手指有 8 根或者 16 根，那么我们的计数方式就会和现在的有所不同。

让我们暂时忘记数字 10 原有的那些特征。假设有一个人有四只鸭子，那么可以他可以简单的用图画表示为：

4 ducks

后来，这个人在想：“我们为什么要画四只鸭子呢？”，于是便又有了下面这幅画：

4 ducks

日子一天天过去，很快这四只鸭子生了很多鸭宝宝，这个人便有个 27 只鸭子，于是便有了下面这幅画：

27 ducks

有一天，一个从欧洲来的旅人对这位农家乐的鸭主人说，你这种画法不具有可持续发展性。于是，这个欧洲人给这个鸭主人画了下面这幅画：

27 roman ducks

这个便是一直沿用至今的罗马数字系统，并由下面这些符号组成：

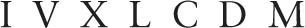
roman numerals

这里 I 表示 1，这可以看作是一个划线或伸出一根手指。字母 V 像一只手，表示 5，两个 V 表示一个 X，代表数字 10。L 是 50，C 表示 100，D 表示 500。最后，M 表示 1000。

如今我们使用的数字系统通常被称为阿拉伯数字，也可以称为印度-阿拉伯数字系统。阿拉伯数字系统起源于印度，被阿拉伯数学家带入欧洲。

阿拉伯数字不同于灵魂画师鸭主人用到的数字系统，主要体现如下三点：

  • 阿拉伯数字系统是和位置相关的。比如 10，和 10,000 这两个数都有 1，而我们知道 10,000 要远大于 10。

  • 比如对于罗马数字系统的符号 X，阿拉伯数字系统没有表示数字 “10”专有符号。

  • 阿拉伯数字有一个数字和数学史上最重要的发明之一，那就是数字“0”。数字“0”支持阿拉伯数字系统的位置计数法，因此我们可将 25、205 和 250 区分开来。

我们可以通过读数字的方式展现阿拉伯数字的整体结构。比如对于数字“4825”，我们可以读做“四千八百二十五”，或者我们可以将其书写如下：

4825 = 4000 + 800 + 20 + 5

或者，对其进一步分解如下：

4825 = 4 x 1000 + 8 x 100 + 2 x 10 + 5

或者，以 10 的整次幂的形式来表示：

4825 = 4 x 10^3 + 8 x 10^2 + 2 x 10^1 + 5 x 10^0

对于我们人类而言，10 是一个非常重要的数字。10 是我们大多数人拥有的手指或脚趾的数目。因为手指非常方便于计数，于是我们已经适应了这个以 10 为基的数字系统。

10 fingers

我们很自然的用数字 10 表示下面这么多鸭子：

10-10-ducks

如果我们人类的手指数目不是 10，我们数数的方式就会不同，那么数字 10 就会有不同的含义。比如数字 10 可以表示下面这么多鸭子：

10-8-ducks

或是这么多鸭子：

10-4-ducks

甚至是这么多鸭子：

10-2-ducks

如果我们人类像卡通人物那样每只手指有 4 根手指，我们可能会自然的创建以 8 为基的数字系统。我们可以用阿拉伯数字系统的 10 个符号中，去掉不需要的符号 9。因为在十进制数中没有特定的符号表示 10，同样，在八进制中，我也不要 8 这个符号。十进制的计数方式是：0 1 2 3 4 5 6 7 8 9，然后是 10。自然地，八进制的计数方式是：0 1 2 3 4 5 6 7 ，然后是 10。

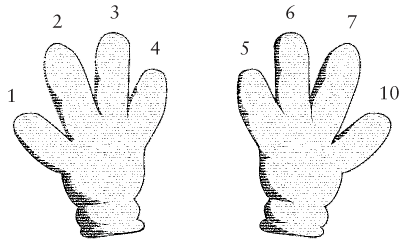
4-fingers-toes

如果继续数脚趾的话，就是下面这样：

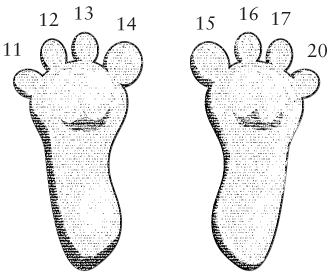
4-feet-toes

同样地，我们有八进制的加法如下：

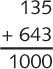
8-octal-number-addition

我们在吃龙虾下的时候，有没有想过，如果我们像龙虾一样有两只前爪，而每只前爪个有两个螯，我们该如何用这四个螯计数我们吃了多少只龙虾呢？

很自然，我们可以设计一个以 4 为基的数字系统，计数方式是：0 1 2 3，然后是 10。

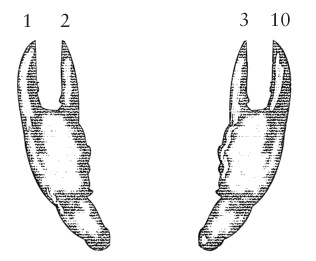
2-front-legs-Lobsters

如果我们是海豚，那么就要使用两个鳍来计数了。我们将创建一个以 2 为基的数字系统，计数方式是：0 1，然后是 10。

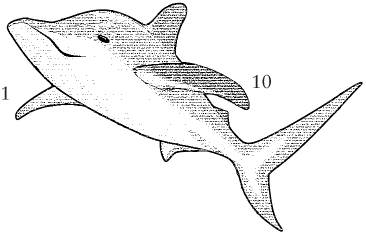
2-bits-dolphins

二进制数只有 0 和 1 这两个符号，因此二进制数最大的问题就是数字用完的很快。比如我们用二进制数十进制的 0 到 10：0 1 10 11 100 101 110 111 1000 1001。

我们可以用十进制，八进制，四进制和二进制计数如下，并发现二进制数的长度增长的很快：

  • 人类的头的个数是 1, 1, 1, 1
  • 海豚身上的鳍的个数是 2, 2, 2, 10
  • 当我们数到 3 只羊时是 3, 3, 3, 11
  • 正方形的边数是 4, 4, 10, 100
  • 人类一只手的手指数是 5, 5, 11, 101
  • 昆虫的腿数是 6, 6, 12, 110
  • 白雪公主遇到的小矮人的数量是 7, 7, 13, 111
  • 八重奏的表演人数是 8, 10, 20, 1000
  • 太阳系的行星总数是 9, 11, 21, 1001
  • 秦皇时期一年的第一个月份是 10, 12, 22, 1010

同样，我们有二进制的加法如下：

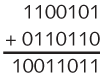
2-binary-number-addition.png

以下是2的个整数幂的几个进制的对应扩展表：

Power of Two Decimal Octal Quaternary Binary
2^0 1 1 1 1
2^1 2 2 2 10
2^2 4 4 10 100
2^3 8 10 20 1000
2^4 16 20 100 10000
2^5 32 40 200 100000
2^6 64 100 1000 1000000
2^7 128 200 2000 10000000
2^8 256 400 10000 100000000
2^9 512 1000 20000 1000000000
2^10 1024 2000 100000 10000000000
2^11 2048 4000 200000 100000000000
2^12 4096 10000 1000000 1000000000000

在这张表中，我们看到有个数字 1024，也就是十进制数 2 的 10 次幂，对应于二进制的整数是 10000000000。

二进制数字系统在算术和电子技术之间架起了一座桥梁。二进制数与计算机之间有着紧密的联系。

大约在 1948 年，美国数学家约翰·威尔德·特克（John Wilder Tukey）就意识到随着计算机的普及，二进制数很可能会在未来发挥更重要的作用。于是他在考虑 bigit，binit后，并最终决定用一个短小、简单、精巧的单词 bit 代替使用起来很不方便的五音节单词 binary digit。

参考

  • Charles Petzold, Code: The Hidden Language of Computer Hardware and Software