Designing Data-Intensive Applications: Consistency and Consensus
The simplest way of handling faults in distributed systems is to simply let the entire service fail, and show the user an error message. If that solution is unacceptable, we need to find ways of tolerating faults—that is, of keeping the service functioning correctly, even if some internal component is faulty.
The best way of building fault-tolerant systems is to find some general-purpose abstractions with useful guarantees, implement them once, and then let applications rely on those guarantees. This is the same approach as we used with transactions: by using a transaction, the application can pretend that there are no crashes (atomicity), that nobody else is concurrently accessing the database (isolation), and that storage devices are perfectly reliable (durability). Even though crashes, race conditions, and disk failures do occur, the transaction abstraction hides those problems so that the application doesn’t need to worry about them.
One of the most important abstractions for distributed systems is consensus: that is, getting all of the nodes to agree on something.
1. Consistency Guarantees
If you look at two nodes in a replicated database at the same moment in time, you’re likely to see different data on the two nodes, because write requests arrive on different nodes at different times. These inconsistencies occur no matter what replication method the database uses (single-leader, multi-leader, or leaderless replication).
Most replicated databases provide at least eventual consistency, which means that if you stop writing to the database and wait for some unspecified length of time, then eventually all read requests will return the same value. In other words, the inconsistency is temporary, and it eventually resolves itself (assuming that any faults in the network are also eventually repaired). A better name for eventual consistency may be convergence, as we expect all replicas to eventually converge to the same value.
However, this is a very weak guarantee—it doesn’t say anything about when the replicas will converge. Until the time of convergence, reads could return anything or nothing.
But, stronger consistency models don’t come for free: systems with stronger guarantees may have worse performance or be less fault-tolerant than systems with weaker guarantees.
2. Linearizability
In an eventually consistent database, if you ask two different replicas the same question at the same time, you may get two different answers. That’s confusing.
The idea behind linearizability (also known as atomic consistency, strong consistency, immediate consistency, or external consistency is to make a system appear as if there were only one copy of the data, and all operations on it are atomic. With this guarantee, even though there may be multiple replicas in reality, the application does not need to worry about them.
In a linearizable system, as soon as one client successfully completes a write, all clients reading from the database must be able to see the value just written. Maintaining the illusion of a single copy of the data means guaranteeing that the value read is the most recent, up-to-date value, and doesn’t come from a stale cache or replica. In other words, linearizability is a recency guarantee.
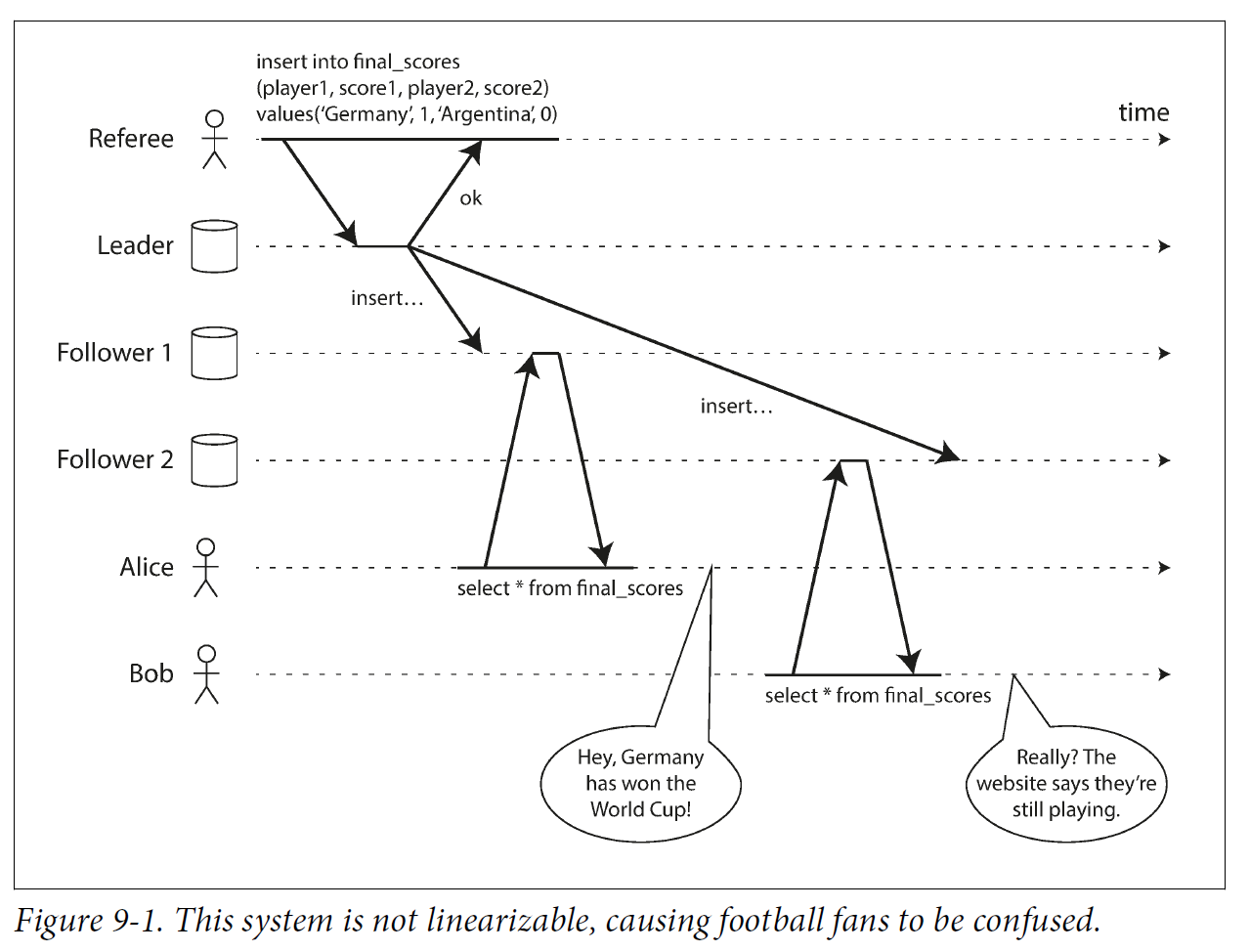
2.1. What Makes a System Linearizable?
The basic idea behind linearizability is simple: to make a system appear as if there is only a single copy of the data.
Figure 9-2 shows three clients concurrently reading and writing the same key x in a linearizable database. In the distributed systems literature, x is called a register—in practice, it could be one key in a key-value store, one row in a relational database, or one document in a document database, for example.
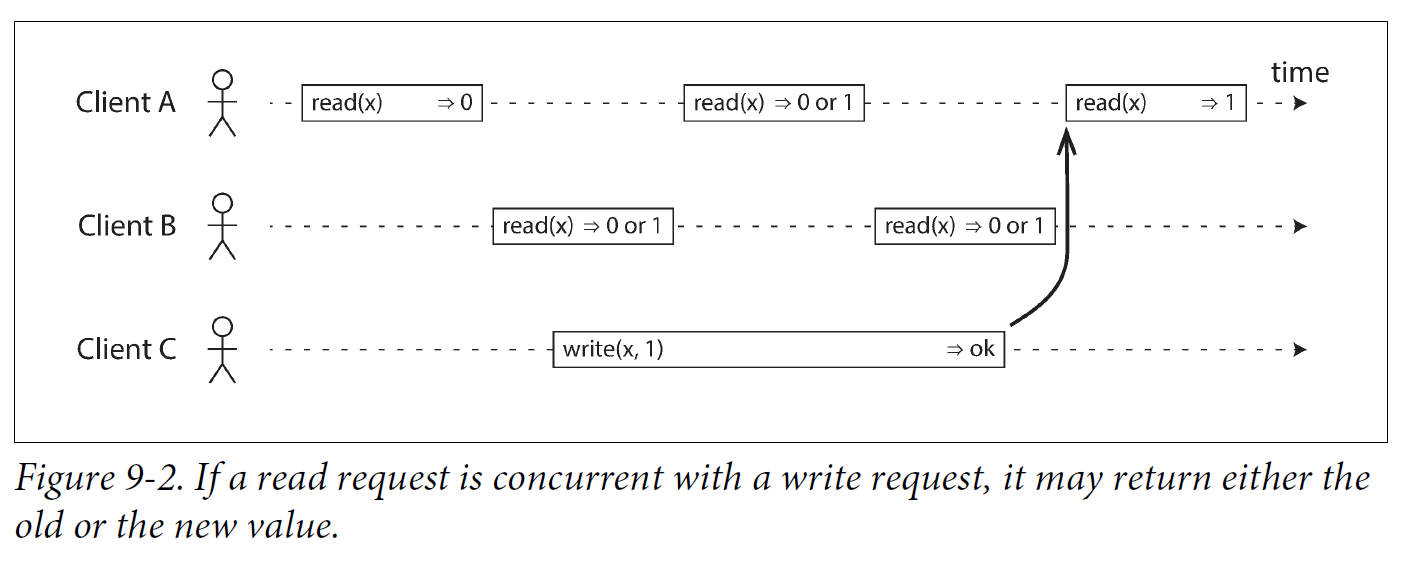
For simplicity, Figure 9-2 shows only the requests from the clients’ point of view, not the internals of the database. Each bar is a request made by a client, where the start of a bar is the time when the request was sent, and the end of a bar is when the response was received by the client. Due to variable network delays, a client doesn’t know exactly when the database processed its request—it only knows that it must have happened sometime between the client sending the request and receiving the response.
In this example, the register has two types of operations:
-
read(x) ⇒ vmeans the client requested to read the value of register x, and the database returned the value v. -
write(x, v) ⇒ rmeans the client requested to set the register x to value v, and the database returned response r (which could be ok or error).
In Figure 9-2, the value of x is initially 0, and client C performs a write request to set it to 1. While this is happening, clients A and B are repeatedly polling the database to read the latest value. What are the possible responses that A and B might get for their read requests?
-
The first read operation by client A completes before the write begins, so it must definitely return the old value 0.
-
The last read by client A begins after the write has completed, so it must definitely return the new value 1 if the database is linearizable: we know that the write must have been processed sometime between the start and end of the write operation, and the read must have been processed sometime between the start and end of the read operation. If the read started after the write ended, then the read must have been processed after the write, and therefore it must see the new value that was written.
-
Any read operations that overlap in time with the write operation might return either 0 or 1, because we don’t know whether or not the write has taken effect at the time when the read operation is processed. These operations are concurrent with the write.
However, that is not yet sufficient to fully describe linearizability: if reads that are concurrent with a write can return either the old or the new value, then readers could see a value flip back and forth between the old and the new value several times while a write is going on. That is not what we expect of a system that emulates a “single copy of the data.”
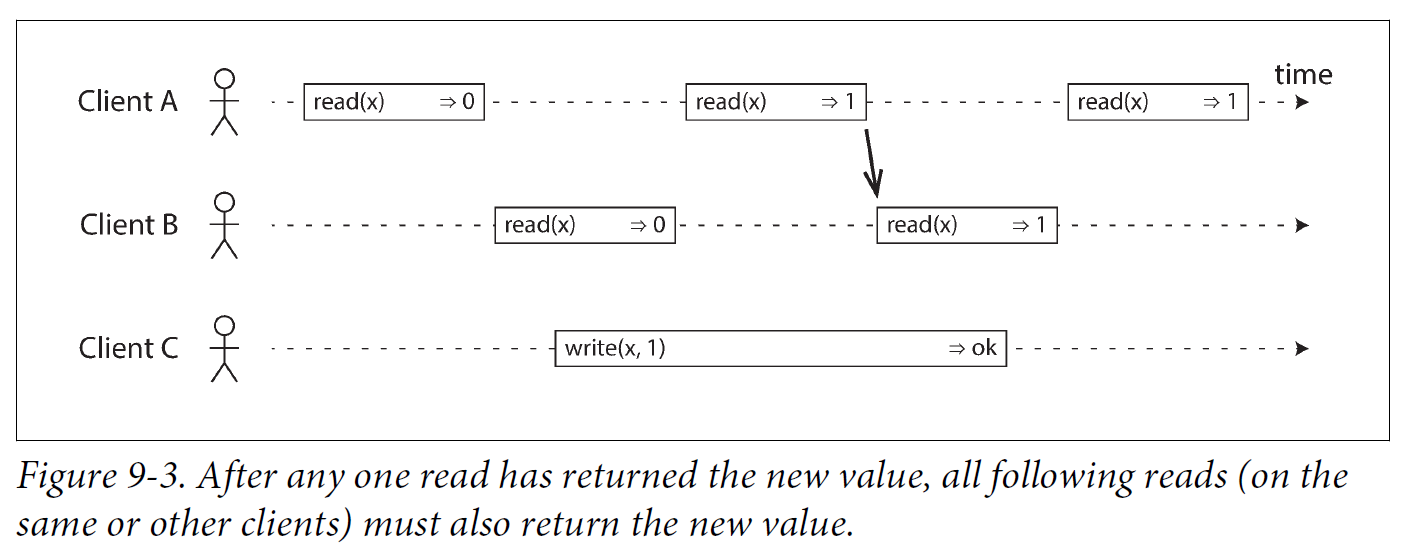
In a linearizable system we imagine that there must be some point in time (between the start and end of the write operation) at which the value of x atomically flips from 0 to 1. Thus, if one client’s read returns the new value 1, all subsequent reads must also return the new value, even if the write operation has not yet completed.
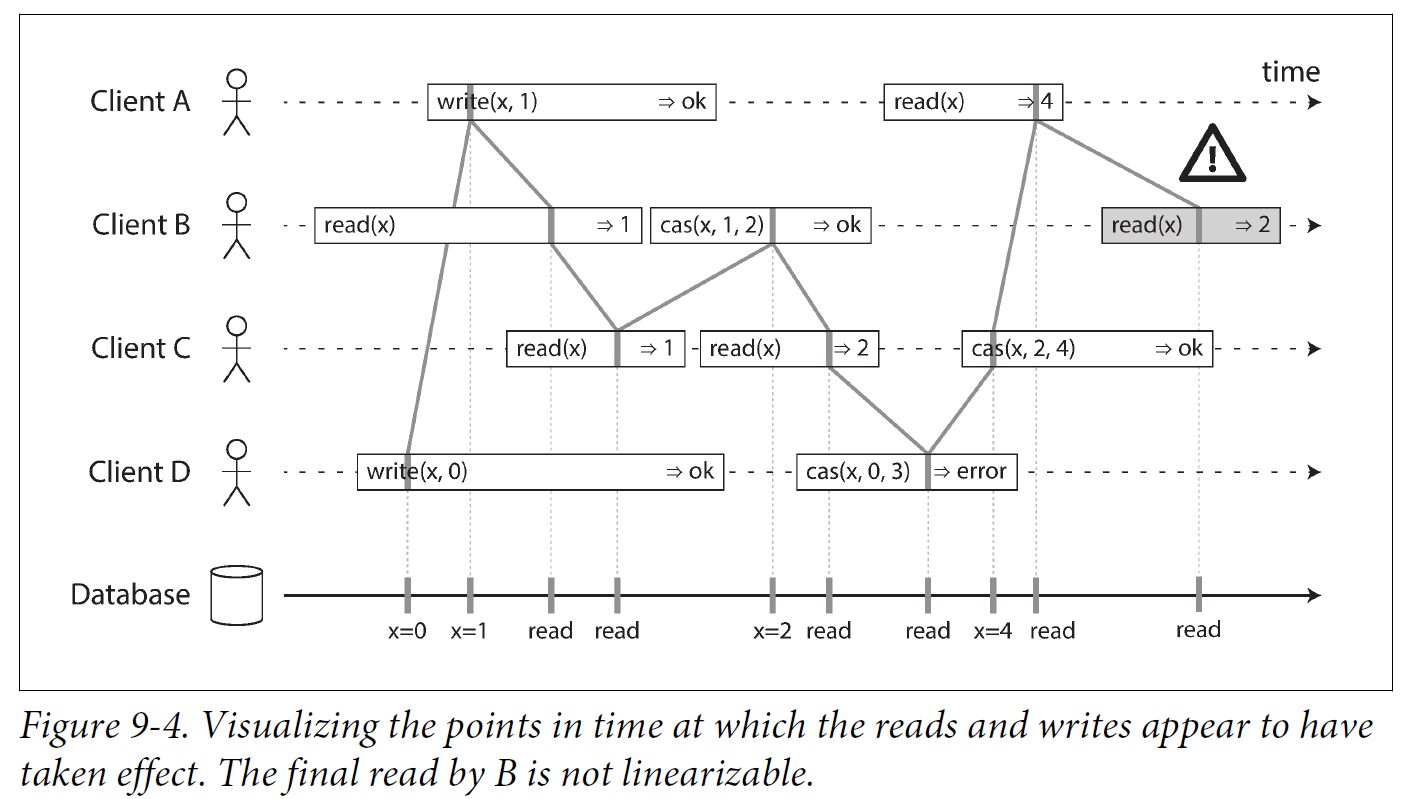
In Figure 9-4 we add a third type of operation besides read and write:
-
cas(x, vold, vnew) ⇒ rmeans the client requested an atomic compare-and-set operation. If the current value of the register x equals vold, it should be atomically set to vnew. If x ≠ vold then the operation should leave the register unchanged and return an error. r is the database’s response (ok or error).
The requirement of linearizability is that the lines joining up the operation markers always move forward in time (from left to right), never backward. This requirement ensures the recency guarantee: once a new value has been written or read, all subsequent reads see the value that was written, until it is overwritten again.
|
Linearizability Versus Serializability
Linearizability is easily confused with serializability, as both words seem to mean something like “can be arranged in a sequential order.” However, they are two quite different guarantees, and it is important to distinguish between them:
A database may provide both serializability and linearizability, and this combination is known as strict serializability or strong one-copy serializability (strong-1SR). Implementations of serializability based on two-phase locking or actual serial execution are typically linearizable. However, serializable snapshot isolation is not linearizable: by design, it makes reads from a consistent snapshot, to avoid lock contention between readers and writers. The whole point of a consistent snapshot is that it does not include writes that are more recent than the snapshot, and thus reads from the snapshot are not linearizable. |
2.2. Relying on Linearizability
-
Locking and leader election
A system that uses single-leader replication needs to ensure that there is indeed only one leader, not several (split brain). One way of electing a leader is to use a lock: every node that starts up tries to acquire the lock, and the one that succeeds becomes the leader. No matter how this lock is implemented, it must be linearizable: all nodes must agree which node owns the lock; otherwise it is useless.
Coordination services like Apache ZooKeeper and etcd are often used to implement distributed locks and leader election. They use consensus algorithms to implement linearizable operations in a fault-tolerant way.
-
Constraints and uniqueness guarantees
Uniqueness constraints are common in databases: for example, a username or email address must uniquely identify one user, and in a file storage service there cannot be two files with the same path and filename. If you want to enforce this constraint as the data is written (such that if two people try to concurrently create a user or a file with the same name, one of them will be returned an error), you need linearizability.
-
Cross-channel timing dependencies
For example, say you have a website where users can upload a photo, and a background process resizes the photos to lower resolution for faster download (thumbnails). The architecture and dataflow of this system is illustrated in Figure 9-5.
The image resizer needs to be explicitly instructed to perform a resizing job, and this instruction is sent from the web server to the resizer via a message queue. The web server doesn’t place the entire photo on the queue, since most message brokers are designed for small messages, and a photo may be several megabytes in size. Instead, the photo is first written to a file storage service, and once the write is complete, the instruction to the resizer is placed on the queue.
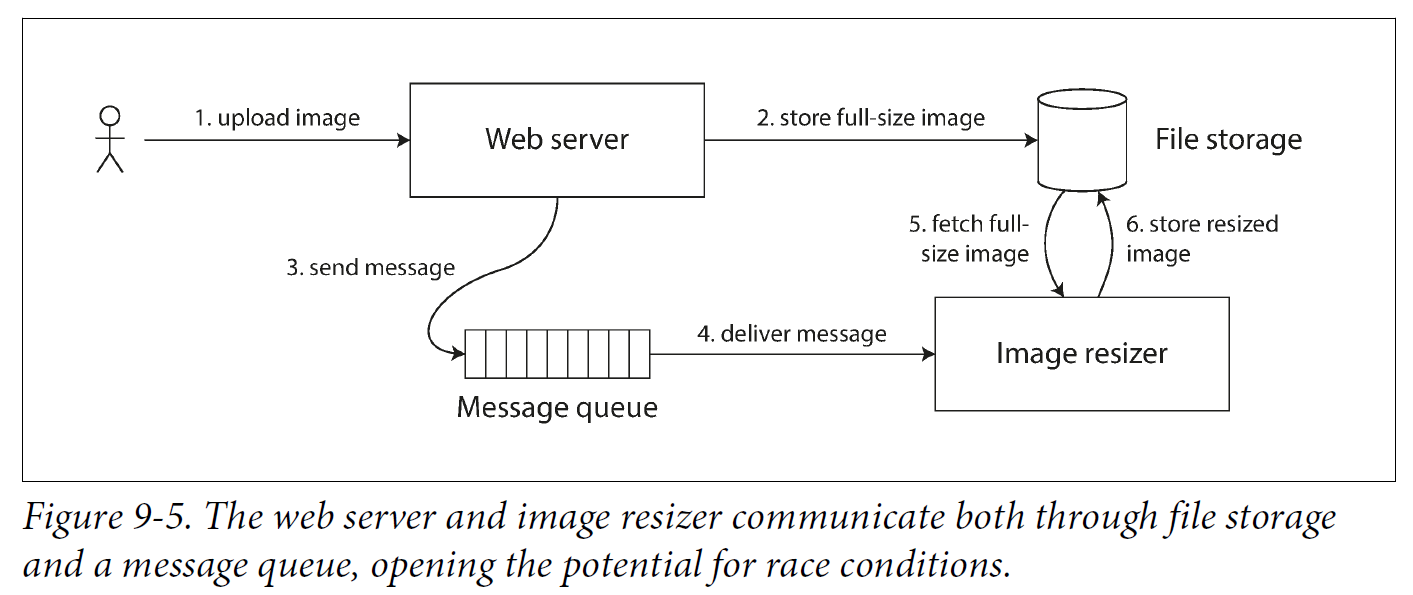
If the file storage service is linearizable, then this system should work fine. If it is not linearizable, there is the risk of a race condition: the message queue (steps 3 and 4 in Figure 9-5) might be faster than the internal replication inside the storage service. In this case, when the resizer fetches the image (step 5), it might see an old version of the image, or nothing at all. If it processes an old version of the image, the full-size and resized images in the file storage become permanently inconsistent.
This problem arises because there are two different communication channels between the web server and the resizer: the file storage and the message queue. Without the recency guarantee of linearizability, race conditions between these two channels are possible.
2.3. Implementing Linearizable Systems
Since linearizability essentially means “behave as though there is only a single copy of the data, and all operations on it are atomic,” the simplest answer would be to really only use a single copy of the data. However, that approach would not be able to tolerate faults: if the node holding that one copy failed, the data would be lost, or at least inaccessible until the node was brought up again.
The most common approach to making a system fault-tolerant is to use replication.
-
Single-leader replication (potentially linearizable)
In a system with single-leader replication, the leader has the primary copy of the data that is used for writes, and the followers maintain backup copies of the data on other nodes. If you make reads from the leader, or from synchronously updated followers, they have the potential to be linearizable. However, not every single-leader database is actually linearizable, either by design (e.g., because it uses snapshot isolation) or due to concurrency bugs.
Using the leader for reads relies on the assumption that you know for sure who the leader is. It is quite possible for a node to think that it is the leader, when in fact it is not—and if the delusional leader continues to serve requests, it is likely to violate linearizability. With asynchronous replication, failover may even lose committed writes, which violates both durability and linearizability.
-
Consensus algorithms (linearizable)
Some consensus algorithms bear a resemblance to single-leader replication. However, consensus protocols contain measures to prevent split brain and stale replicas. Thanks to these details, consensus algorithms can implement linearizable storage safely. This is how ZooKeeper and etcd work, for example.
-
Multi-leader replication (not linearizable)
Systems with multi-leader replication are generally not linearizable, because they concurrently process writes on multiple nodes and asynchronously replicate them to other nodes. For this reason, they can produce conflicting writes that require resolution. Such conflicts are an artifact of the lack of a single copy of the data.
-
Leaderless replication (probably not linearizable)
For systems with leaderless replication (Dynamo-style), people sometimes claim that you can obtain “strong consistency” by requiring quorum reads and writes (w + r > n). Depending on the exact configuration of the quorums, and depending on how you define strong consistency, this is not quite true.
“Last write wins” conflict resolution methods based on time-of-day clocks (e.g., in Cassandra) are almost certainly nonlinearizable, because clock timestamps cannot be guaranteed to be consistent with actual event ordering due to clock skew. Sloppy quorums also ruin any chance of linearizability. Even with strict quorums, nonlinearizable behavior is possible.
Intuitively, it seems as though strict quorum reads and writes should be linearizable in a Dynamo-style model. However, when we have variable network delays, it is possible to have race conditions.
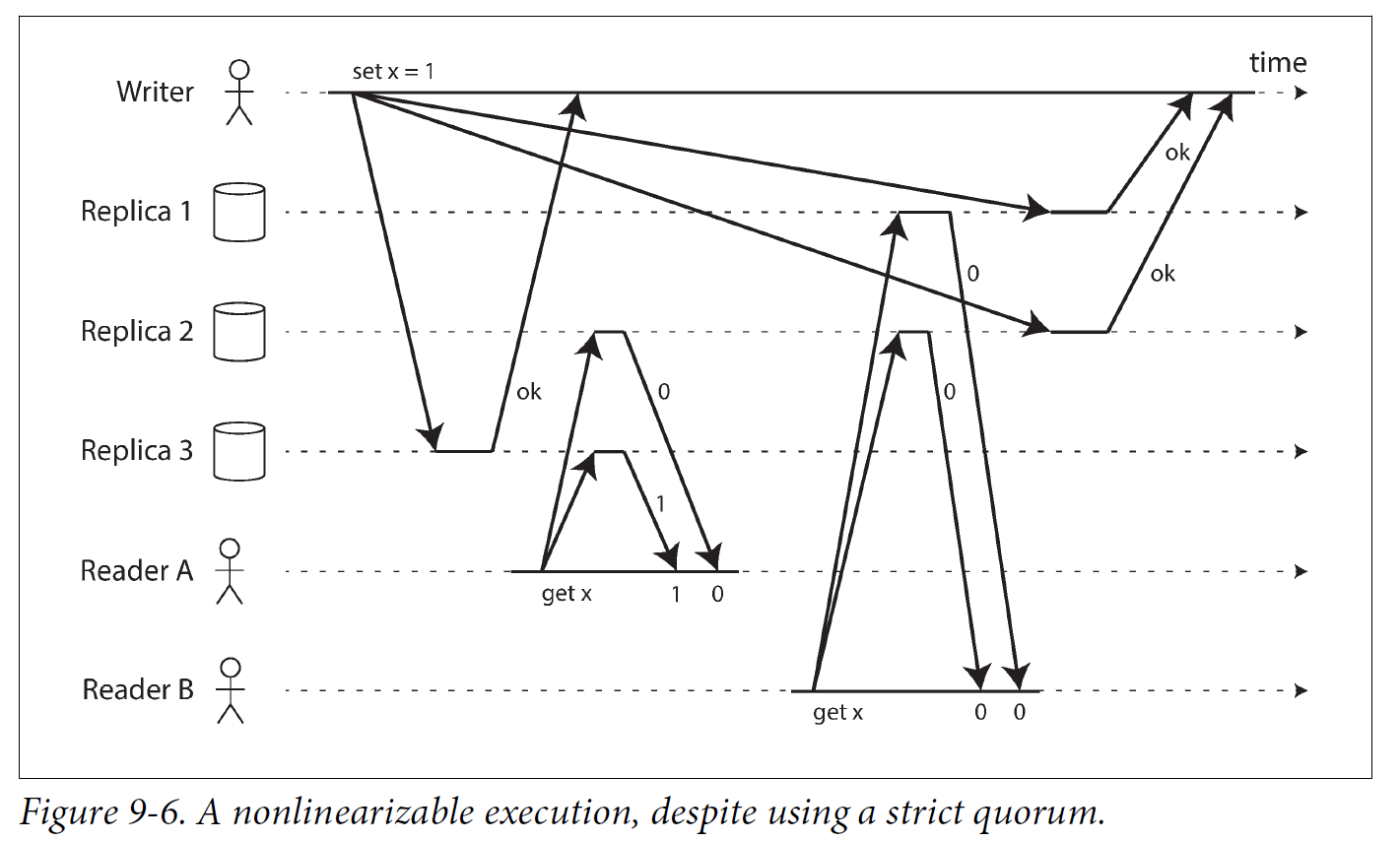
In summary, it is safest to assume that a leaderless system with Dynamo-style replication does not provide linearizability.
2.4. The Cost of Linearizability
2.4.1. The CAP theorem
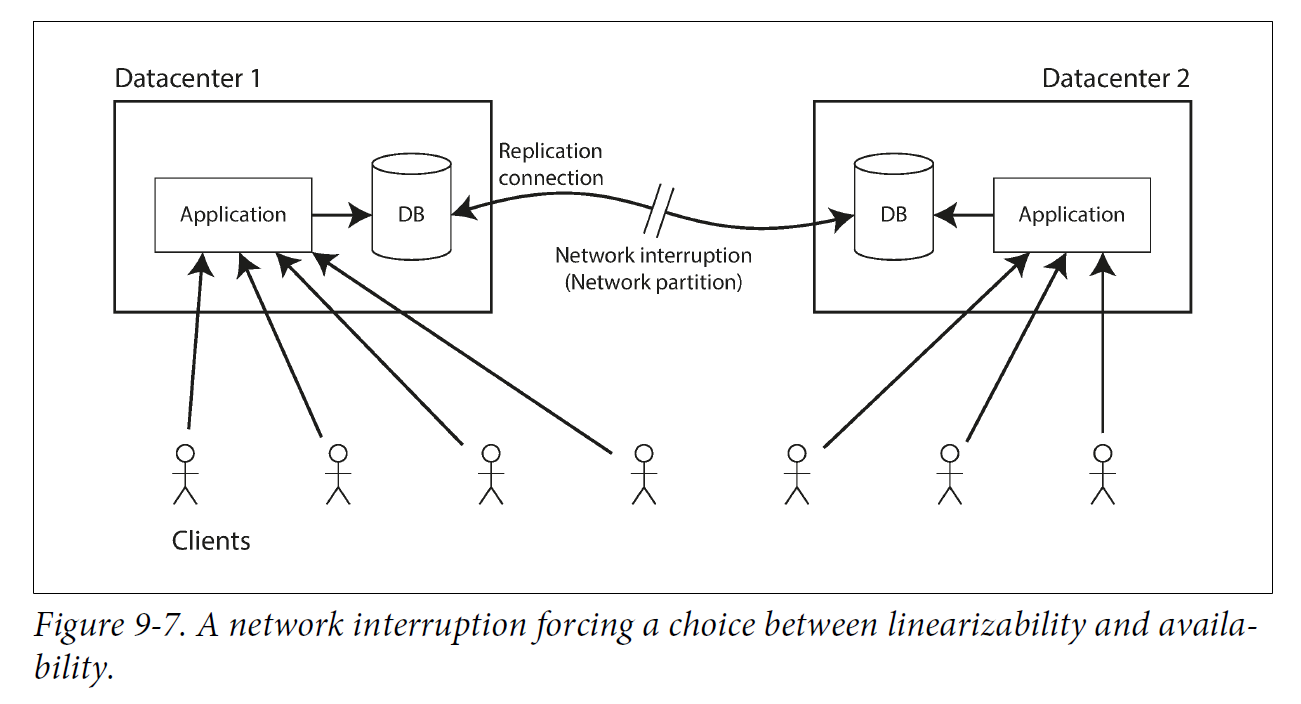
-
If your application requires linearizability, and some replicas are disconnected from the other replicas due to a network problem, then some replicas cannot process requests while they are disconnected: they must either wait until the network problem is fixed, or return an error (either way, they become unavailable).
-
If your application does not require linearizability, then it can be written in a way that each replica can process requests independently, even if it is disconnected from other replicas (e.g., multi-leader). In this case, the application can remain available in the face of a network problem, but its behavior is not linearizable.
Thus, applications that don’t require linearizability can be more tolerant of network problems. This insight is popularly known as the CAP theorem, named by Eric Brewer in 2000, although the trade-off has been known to designers of distributed databases since the 1970s.
|
The Unhelpful CAP Theorem
CAP is sometimes presented as Consistency, Availability, Partition tolerance: pick 2 out of 3. Unfortunately, putting it this way is misleading because network partitions are a kind of fault, so they aren’t something about which you have a choice: they will happen whether you like it or not. At times when the network is working correctly, a system can provide both consistency (linearizability) and total availability. When a network fault occurs, you have to choose between either linearizability or total availability. Thus, a better way of phrasing CAP would be either Consistent or Available when Partitioned. A more reliable network needs to make this choice less often, but at some point the choice is inevitable. In discussions of CAP there are several contradictory definitions of the term availability, and the formalization as a theorem does not match its usual meaning. Many so-called “highly available” (fault-tolerant) systems actually do not meet CAP’s idiosyncratic definition of availability. All in all, there is a lot of misunderstanding and confusion around CAP, and it does not help us understand systems better, so CAP is best avoided. |
The CAP theorem as formally defined [30] is of very narrow scope: it only considers one consistency model (namely linearizability) and one kind of fault (network partitions, vi or nodes that are alive but disconnected from each other).
2.4.2. Linearizability and network delays
Although linearizability is a useful guarantee, surprisingly few systems are actually linearizable in practice. For example, even RAM on a modern multi-core CPU is not linearizable: if a thread running on one CPU core writes to a memory address, and a thread on another CPU core reads the same address shortly afterward, it is not guaranteed to read the value written by the first thread (unless a memory barrier or fence is used).
The reason for this behavior is that every CPU core has its own memory cache and store buffer. Memory access first goes to the cache by default, and any changes are asynchronously written out to main memory. Since accessing data in the cache is much faster than going to main memory, this feature is essential for good performance on modern CPUs. However, there are now several copies of the data (one in main memory, and perhaps several more in various caches), and these copies are asynchronously updated, so linearizability is lost.
Why make this trade-off? It makes no sense to use the CAP theorem to justify the multi-core memory consistency model: within one computer we usually assume reliable communication, and we don’t expect one CPU core to be able to continue operating normally if it is disconnected from the rest of the computer. The reason for dropping linearizability is performance, not fault tolerance.
The same is true of many distributed databases that choose not to provide linearizable guarantees: they do so primarily to increase performance, not so much for fault tolerance. Linearizability is slow—and this is true all the time, not only during a network fault.
Can’t we maybe find a more efficient implementation of linearizable storage? It seems the answer is no: Attiya and Welch prove that if you want linearizability, the response time of read and write requests is at least proportional to the uncertainty of delays in the network. In a network with highly variable delays, like most computer networks, the response time of linearizable reads and writes is inevitably going to be high. A faster algorithm for linearizability does not exist, but weaker consistency models can be much faster, so this trade-off is important for latency-sensitive systems.
3. Ordering Guarantees
-
The main purpose of the leader in single-leader replication is to determine the order of writes in the replication log—that is, the order in which followers apply those writes.
-
Serializability is about ensuring that transactions behave as if they were executed in some sequential order. It can be achieved by literally executing transactions in that serial order, or by allowing concurrent execution while preventing serialization conflicts (by locking or aborting).
-
The use of timestamps and clocks in distributed systems is another attempt to introduce order into a disorderly world, for example to determine which one of two writes happened later.
3.1. Ordering and Causality
Causality imposes an ordering on events: cause comes before effect; a message is sent before that message is received; the question comes before the answer. And, like in real life, one thing leads to another: one node reads some data and then writes something as a result, another node reads the thing that was written and writes something else in turn, and so on. These chains of causally dependent operations define the causal order in the system—i.e., what happened before what.
3.1.1. The causal order is not a total order
A total order allows any two elements to be compared, so if you have two elements, you can always say which one is greater and which one is smaller. For example, natural numbers are totally ordered: if I give you any two numbers, say 5 and 13, you can tell me that 13 is greater than 5.
However, mathematical sets are not totally ordered: is {a, b} greater than {b, c}? Well, you can’t really compare them, because neither is a subset of the other. We say they are incomparable, and therefore mathematical sets are partially ordered: in some cases one set is greater than another (if one set contains all the elements of another), but in other cases they are incomparable.
-
Linearizability
In a linearizable system, we have a total order of operations: if the system behaves as if there is only a single copy of the data, and every operation is atomic, this means that for any two operations we can always say which one happened first.
-
Causality
We said that two operations are concurrent if neither happened before the other. Put another way, two events are ordered if they are causally related (one happened before the other), but they are incomparable if they are concurrent. This means that causality defines a partial order, not a total order: some operations are ordered with respect to each other, but some are incomparable.
Therefore, according to this definition, there are no concurrent operations in a linearizable datastore: there must be a single timeline along which all operations are totally ordered. There might be several requests waiting to be handled, but the datastore ensures that every request is handled atomically at a single point in time, acting on a single copy of the data, along a single timeline, without any concurrency.
3.1.2. Linearizability is stronger than causal consistency
So what is the relationship between the causal order and linearizability? The answer is any system that is linearizable will preserve causality correctly.
The fact that linearizability ensures causality is what makes linearizable systems simple to understand and appealing. However making a system linearizable can harm its performance and availability, especially if the system has significant network delays (for example, if it’s geographically distributed). For this reason, some distributed data systems have abandoned linearizability, which allows them to achieve better performance but can make them difficult to work with.
In many cases, systems that appear to require linearizability in fact only really require causal consistency, which can be implemented more efficiently. In fact, causal consistency is the strongest possible consistency model that does not slow down due to network delays, and remains available in the face of network failures.
3.1.3. Capturing causal dependencies
In order to maintain causality, you need to know which operation happened before which other operation. This is a partial order: concurrent operations may be processed in any order, but if one operation happened before another, then they must be processed in that order on every replica. Thus, when a replica processes an operation, it must ensure that all causally preceding operations (all operations that happened before) have already been processed; if some preceding operation is missing, the later operation must wait until the preceding operation has been processed.
3.2. Sequence Number Ordering
Although causality is an important theoretical concept, actually keeping track of all causal dependencies can become impractical. In many applications, clients read lots of data before writing something, and then it is not clear whether the write is causally dependent on all or only some of those prior reads. Explicitly tracking all the data that has been read would mean a large overhead.
However, there is a better way: we can use sequence numbers or timestamps to order events. A timestamp need not come from a time-of-day clock (or physical clock, which have many problems. It can instead come from a logical clock, which is an algorithm to generate a sequence of numbers to identify operations, typically using counters that are incremented for every operation.
Such sequence numbers or timestamps are compact (only a few bytes in size), and they provide a total order: that is, every operation has a unique sequence number, and you can always compare two sequence numbers to determine which is greater (i.e., which operation happened later).
In particular, we can create sequence numbers in a total order that is consistent with causality: we promise that if operation A causally happened before B, then A occurs before B in the total order (A has a lower sequence number than B). Concurrent operations may be ordered arbitrarily. Such a total order captures all the causality information, but also imposes more ordering than strictly required by causality.
In a database with single-leader replication, the replication log defines a total order of write operations that is consistent with causality. The leader can simply increment a counter for each operation, and thus assign a monotonically increasing sequence number to each operation in the replication log. If a follower applies the writes in the order they appear in the replication log, the state of the follower is always causally consistent (even if it is lagging behind the leader).
3.2.1. Noncausal sequence number generators
If there is not a single leader (perhaps because you are using a multi-leader or leaderless database, or because the database is partitioned), it is less clear how to generate sequence numbers for operations. Various methods are used in practice:
-
Each node can generate its own independent set of sequence numbers. For example, if you have two nodes, one node can generate only odd numbers and the other only even numbers. In general, you could reserve some bits in the binary representation of the sequence number to contain a unique node identifier, and this would ensure that two different nodes can never generate the same sequence number.
-
You can attach a timestamp from a time-of-day clock (physical clock) to each operation. Such timestamps are not sequential, but if they have sufficiently high resolution, they might be sufficient to totally order operations. This fact is used in the last write wins conflict resolution method.
-
You can preallocate blocks of sequence numbers. For example, node A might claim the block of sequence numbers from 1 to 1,000, and node B might claim the block from 1,001 to 2,000. Then each node can independently assign sequence numbers from its block, and allocate a new block when its supply of sequence numbers begins to run low.
These three options all perform better and are more scalable than pushing all operations through a single leader that increments a counter. They generate a unique, approximately increasing sequence number for each operation. However, they all have a problem: the sequence numbers they generate are not consistent with causality.
3.2.2. Lamport timestamps
Although the three sequence number generators just described are inconsistent with causality, there is actually a simple method for generating sequence numbers that is consistent with causality. It is called a Lamport timestamp, proposed in 1978 by Leslie Lamport, in what is now one of the most-cited papers in the field of distributed systems.
The use of Lamport timestamps is illustrated in Figure 9-8. Each node has a unique identifier, and each node keeps a counter of the number of operations it has processed. The Lamport timestamp is then simply a pair of (counter, node ID). Two nodes may sometimes have the same counter value, but by including the node ID in the timestamp, each timestamp is made unique.
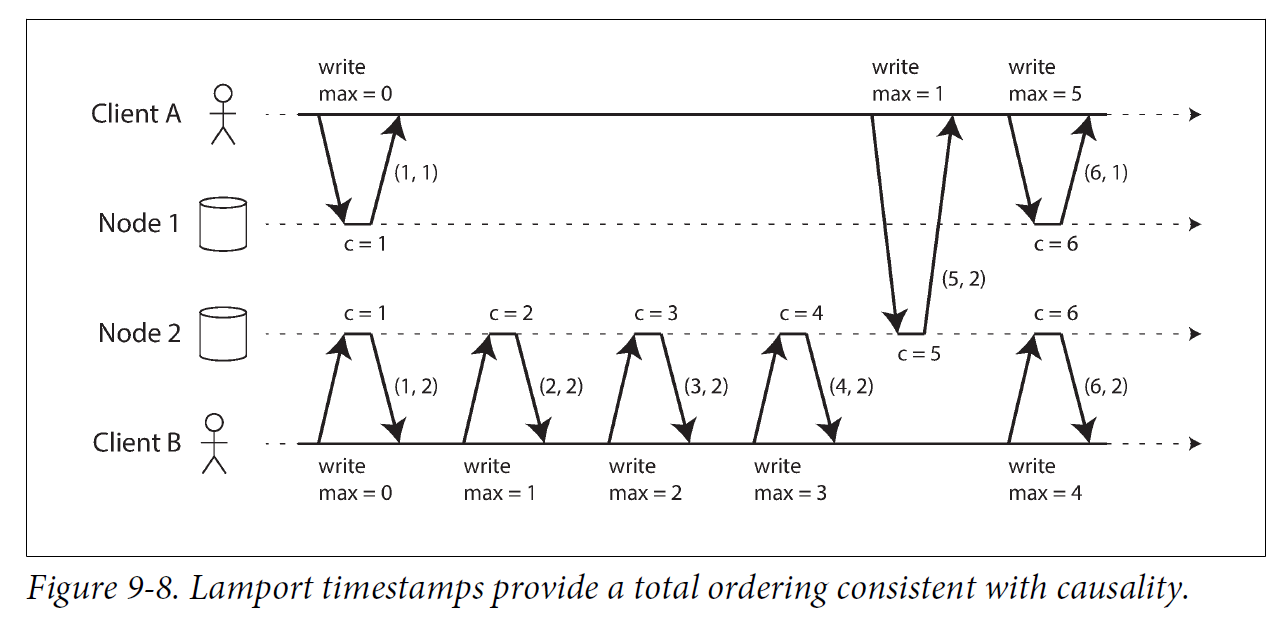
A Lamport timestamp bears no relationship to a physical time-of-day clock, but it provides total ordering: if you have two timestamps, the one with a greater counter value is the greater timestamp; if the counter values are the same, the one with the greater node ID is the greater timestamp.
The key idea about Lamport timestamps, which makes them consistent with causality, is the following: every node and every client keeps track of the maximum counter value it has seen so far, and includes that maximum on every request. When a node receives a request or response with a maximum counter value greater than its own counter value, it immediately increases its own counter to that maximum.
3.2.3. Timestamp ordering is not sufficient
Although Lamport timestamps define a total order of operations that is consistent with causality, they are not quite sufficient to solve many common problems in distributed systems.
For example, consider a system that needs to ensure that a username uniquely identifies a user account. If two users concurrently try to create an account with the same username, one of the two should succeed and the other should fail.
At first glance, it seems as though a total ordering of operations (e.g., using Lamport timestamps) should be sufficient to solve this problem: if two accounts with the same username are created, pick the one with the lower timestamp as the winner (the one who grabbed the username first), and let the one with the greater timestamp fail. Since timestamps are totally ordered, this comparison is always valid.
In order to be sure that no other node is in the process of concurrently creating an account with the same username and a lower timestamp, you would have to check with every other node to see what it is doing. If one of the other nodes has failed or cannot be reached due to a network problem, this system would grind to a halt. This is not the kind of fault-tolerant system that we need.
To conclude: in order to implement something like a uniqueness constraint for usernames, it’s not sufficient to have a total ordering of operations—you also need to know when that order is finalized. If you have an operation to create a username, and you are sure that no other node can insert a claim for the same username ahead of your operation in the total order, then you can safely declare the operation successful.
3.3. Total Order Broadcast
If your program runs only on a single CPU core, it is easy to define a total ordering of operations: it is simply the order in which they were executed by the CPU. However, in a distributed system, getting all nodes to agree on the same total ordering of operations is tricky.
Total order broadcast or atomic broadcast is usually described as a protocol for exchanging messages between nodes. Informally, it requires that two safety properties always be satisfied:
-
Reliable delivery
No messages are lost: if a message is delivered to one node, it is delivered to all nodes.
-
Totally ordered delivery
Messages are delivered to every node in the same order.
A correct algorithm for total order broadcast must ensure that the reliability and ordering properties are always satisfied, even if a node or the network is faulty. Of course, messages will not be delivered while the network is interrupted, but an algorithm can keep retrying so that the messages get through when the network is eventually repaired (and then they must still be delivered in the correct order).
|
Partitioned databases with a single leader per partition often maintain ordering only per partition, which means they cannot offer consistency guarantees (e.g., consistent snapshots, foreign key references) across partitions. Total ordering across all partitions is possible, but requires additional coordination. |
3.3.1. Using total order broadcast
Consensus services such as ZooKeeper and etcd actually implement total order broadcast. This fact is a hint that there is a strong connection between total order broadcast and consensus.
Total order broadcast is exactly what you need for database replication: if every message represents a write to the database, and every replica processes the same writes in the same order, then the replicas will remain consistent with each other (aside from any temporary replication lag). This principle is known as state machine replication.
Similarly, total order broadcast can be used to implement serializable transactions: if every message represents a deterministic transaction to be executed as a stored procedure, and if every node processes those messages in the same order, then the partitions and replicas of the database are kept consistent with each other.
An important aspect of total order broadcast is that the order is fixed at the time the messages are delivered: a node is not allowed to retroactively insert a message into an earlier position in the order if subsequent messages have already been delivered. This fact makes total order broadcast stronger than timestamp ordering.
Another way of looking at total order broadcast is that it is a way of creating a log (as in a replication log, transaction log, or write-ahead log): delivering a message is like appending to the log. Since all nodes must deliver the same messages in the same order, all nodes can read the log and see the same sequence of messages.
Total order broadcast is also useful for implementing a lock service that provides fencing tokens. Every request to acquire the lock is appended as a message to the log, and all messages are sequentially numbered in the order they appear in the log. The sequence number can then serve as a fencing token, because it is monotonically increasing. In ZooKeeper, this sequence number is called zxid.
3.3.2. Implementing linearizable storage using total order broadcast
Total order broadcast is asynchronous: messages are guaranteed to be delivered reliably in a fixed order, but there is no guarantee about when a message will be delivered (so one recipient may lag behind the others). By contrast, linearizability is a recency guarantee: a read is guaranteed to see the latest value written.
However, if you have total order broadcast, you can build linearizable storage on top of it. For example, you can ensure that usernames uniquely identify user accounts.
Imagine that for every possible username, you can have a linearizable register with an atomic compare-and-set operation. Every register initially has the value null (indicating that the username is not taken). When a user wants to create a username, you execute a compare-and-set operation on the register for that username, setting it to the user account ID, under the condition that the previous register value is null. If multiple users try to concurrently grab the same username, only one of the compare-and-set operations will succeed, because the others will see a value other than null (due to linearizability).
3.3.3. Implementing total order broadcast using linearizable storage
The algorithm is simple: for every message you want to send through total order broadcast, you increment-and-get the linearizable integer, and then attach the value you got from the register as a sequence number to the message. You can then send the message to all nodes (resending any lost messages), and the recipients will deliver the messages consecutively by sequence number.
How hard could it be to make a linearizable integer with an atomic increment-and-get operation? As usual, if things never failed, it would be easy: you could just keep it in a variable on one node. The problem lies in handling the situation when network connections to that node are interrupted, and restoring the value when that node fails. In general, if you think hard enough about linearizable sequence number generators, you inevitably end up with a consensus algorithm.
4. Distributed Transactions and Consensus
Consensus is one of the most important and fundamental problems in distributed computing. On the surface, it seems simple: informally, the goal is simply to get several nodes to agree on something. You might think that this shouldn’t be too hard. Unfortunately, many broken systems have been built in the mistaken belief that this problem is easy to solve.
There are a number of situations in which it is important for nodes to agree. For example:
-
Leader election
In a database with single-leader replication, all nodes need to agree on which node is the leader. The leadership position might become contested if some nodes can’t communicate with others due to a network fault. In this case, consensus is important to avoid a bad failover, resulting in a split brain situation in which two nodes both believe themselves to be the leader. If there were two leaders, they would both accept writes and their data would diverge, leading to inconsistency and data loss.
-
Atomic commit
In a database that supports transactions spanning several nodes or partitions, we have the problem that a transaction may fail on some nodes but succeed on others. If we want to maintain transaction atomicity, we have to get all nodes to agree on the outcome of the transaction: either they all abort/roll back (if anything goes wrong) or they all commit (if nothing goes wrong). This instance of consensus is known as the atomic commit problem.
|
The Impossibility of Consensus
You may have heard about the FLP result—named after the authors Fischer, Lynch, and Paterson—which proves that there is no algorithm that is always able to reach consensus if there is a risk that a node may crash. In a distributed system, we must assume that nodes may crash, so reliable consensus is impossible. Yet, here we are, discussing algorithms for achieving consensus. What is going on here? The answer is that the FLP result is proved in the asynchronous system model, a very restrictive model that assumes a deterministic algorithm that cannot use any clocks or timeouts. If the algorithm is allowed to use timeouts, or some other way of identifying suspected crashed nodes (even if the suspicion is sometimes wrong), then consensus becomes solvable. Even just allowing the algorithm to use random numbers is sufficient to get around the impossibility result. Thus, although the FLP result about the impossibility of consensus is of great theoretical importance, distributed systems can usually achieve consensus in practice. |
By learning from two-phase commit (2PC) algorithm, which is the most common way of solving atomic commit, we will then work our way toward better consensus algorithms, such as those used in ZooKeeper (Zab) and etcd (Raft).
4.1. Atomic Commit and Two-Phase Commit (2PC)
Atomicity prevents failed transactions from littering the database with half-finished results and half-updated state.
4.1.1. From single-node to distributed atomic commit
For transactions that execute at a single database node, atomicity is commonly implemented by the storage engine. When the client asks the database node to commit the transaction, the database makes the transaction’s writes durable (typically in a write-ahead log) and then appends a commit record to the log on disk. If the database crashes in the middle of this process, the transaction is recovered from the log when the node restarts: if the commit record was successfully written to disk before the crash, the transaction is considered committed; if not, any writes from that transaction are rolled back.
Thus, on a single node, transaction commitment crucially depends on the order in which data is durably written to disk: first the data, then the commit record. The key deciding moment for whether the transaction commits or aborts is the moment at which the disk finishes writing the commit record: before that moment, it is still possible to abort (due to a crash), but after that moment, the transaction is committed (even if the database crashes). Thus, it is a single device (the controller of one particular disk drive, attached to one particular node) that makes the commit atomic.
A transaction commit must be irrevocable—you are not allowed to change your mind and retroactively abort a transaction after it has been committed. The reason for this rule is that once data has been committed, it becomes visible to other transactions, and thus other clients may start relying on that data; this principle forms the basis of read committed isolation. It is possible for the effects of a committed transaction to later be undone by another, compensating transaction. However, from the database’s point of view this is a separate transaction, and thus any cross-transaction correctness requirements are the application’s problem.
4.1.2. Introduction to two-phase commit
Two-phase commit is an algorithm for achieving atomic transaction commit across multiple nodes—i.e., to ensure that either all nodes commit or all nodes abort. It is a classic algorithm in distributed databases.
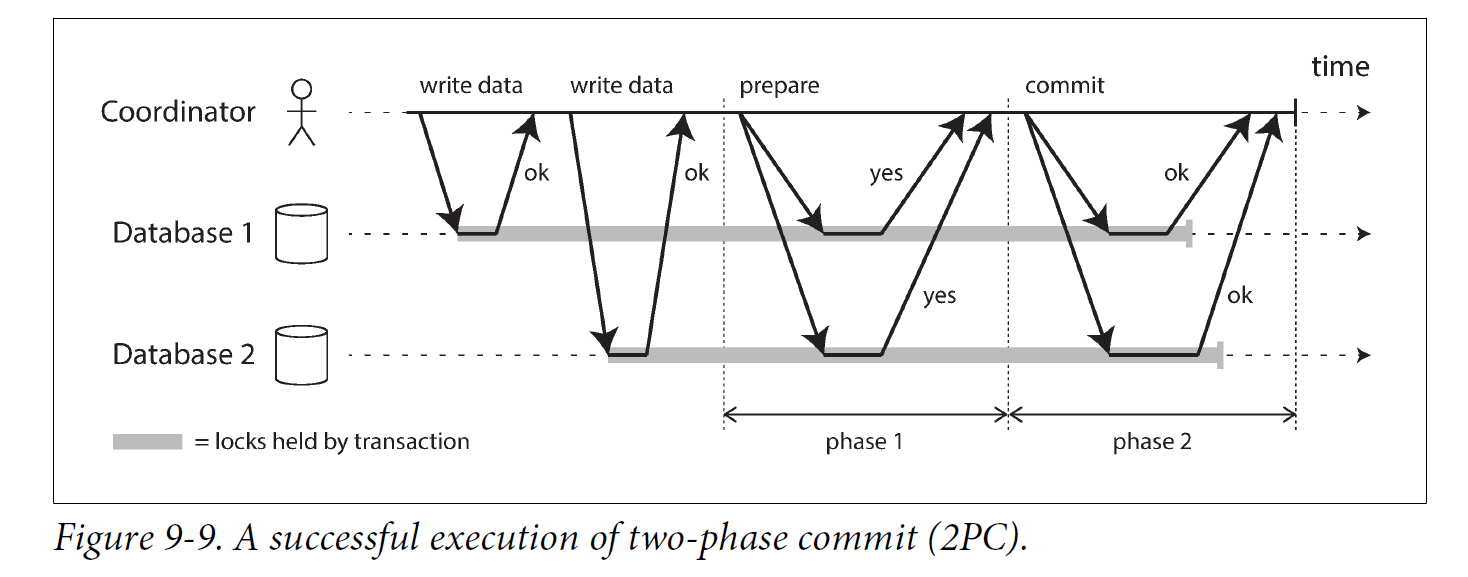
2PC uses a new component that does not normally appear in single-node transactions: a coordinator (also known as transaction manager). The coordinator is often implemented as a library within the same application process that is requesting the transaction (e.g., embedded in a Java EE container), but it can also be a separate process or service.
A 2PC transaction begins with the application reading and writing data on multiple database nodes, as normal. We call these database nodes participants in the transaction. When the application is ready to commit, the coordinator begins phase 1: it sends a prepare request to each of the nodes, asking them whether they are able to commit. The coordinator then tracks the responses from the participants:
-
If all participants reply “yes,” indicating they are ready to commit, then the coordinator sends out a commit request in phase 2, and the commit actually takes place.
-
If any of the participants replies “no,” the coordinator sends an abort request to all nodes in phase 2.
A system of promises
To understand why it works, we have to break down the process in a bit more detail:
-
When the application wants to begin a distributed transaction, it requests a transaction ID from the coordinator. This transaction ID is globally unique.
-
The application begins a single-node transaction on each of the participants, and attaches the globally unique transaction ID to the single-node transaction. All reads and writes are done in one of these single-node transactions. If anything goes wrong at this stage (for example, a node crashes or a request times out), the coordinator or any of the participants can abort.
-
When the application is ready to commit, the coordinator sends a prepare request to all participants, tagged with the global transaction ID. If any of these requests fails or times out, the coordinator sends an abort request for that transaction ID to all participants.
-
When a participant receives the prepare request, it makes sure that it can definitely commit the transaction under all circumstances. This includes writing all transaction data to disk (a crash, a power failure, or running out of disk space is not an acceptable excuse for refusing to commit later), and checking for any conflicts or constraint violations. By replying “yes” to the coordinator, the node promises to commit the transaction without error if requested. In other words, the participant surrenders the right to abort the transaction, but without actually committing it.
-
When the coordinator has received responses to all prepare requests, it makes a definitive decision on whether to commit or abort the transaction (committing only if all participants voted “yes”). The coordinator must write that decision to its transaction log on disk so that it knows which way it decided in case it subsequently crashes. This is called the commit point.
-
Once the coordinator’s decision has been written to disk, the commit or abort request is sent to all participants. If this request fails or times out, the coordinator must retry forever until it succeeds. There is no more going back: if the decision was to commit, that decision must be enforced, no matter how many retries it takes. If a participant has crashed in the meantime, the transaction will be committed when it recovers—since the participant voted “yes,” it cannot refuse to commit when it recovers.
Coordinator failure
If the coordinator fails before sending the prepare requests, a participant can safely abort the transaction. But once the participant has received a prepare request and voted “yes,” it can no longer abort unilaterally—it must wait to hear back from the coordinator whether the transaction was committed or aborted. If the coordinator crashes or the network fails at this point, the participant can do nothing but wait. A participant’s transaction in this state is called in doubt or uncertain.
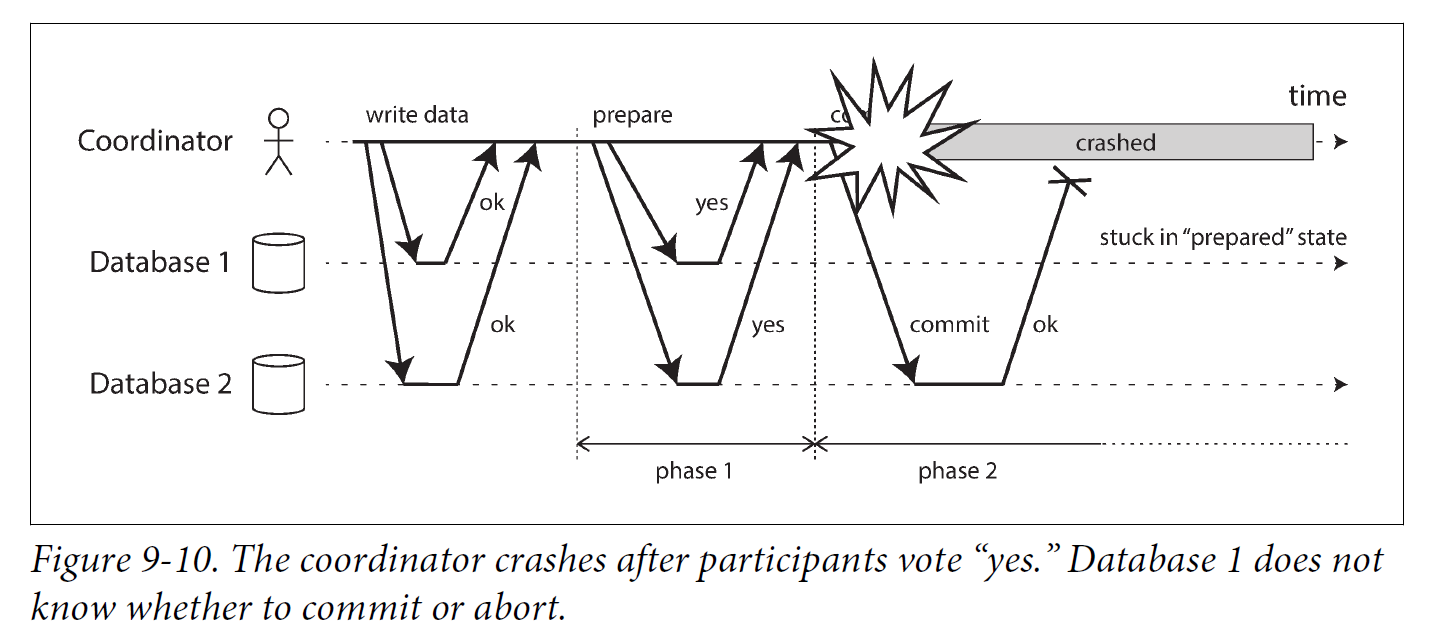
The only way 2PC can complete is by waiting for the coordinator to recover. This is why the coordinator must write its commit or abort decision to a transaction log on disk before sending commit or abort requests to participants: when the coordinator recovers, it determines the status of all in-doubt transactions by reading its transaction log. Any transactions that don’t have a commit record in the coordinator’s log are aborted. Thus, the commit point of 2PC comes down to a regular single-node atomic commit on the coordinator.
4.1.3. Distributed Transactions in Practice
Distributed transactions, especially those implemented with two-phase commit, have a mixed reputation. On the one hand, they are seen as providing an important safety guarantee that would be hard to achieve otherwise; on the other hand, they are criticized for causing operational problems, killing performance, and promising more than they can deliver.
-
Database-internal distributed transactions
Some distributed databases (i.e., databases that use replication and partitioning in their standard configuration) support internal transactions among the nodes of that database.
-
Heterogeneous distributed transactions
In a heterogeneous transaction, the participants are two or more different technologies: for example, two databases from different vendors, or even nondatabase systems such as message brokers. A distributed transaction across these systems must ensure atomic commit, even though the systems may be entirely different under the hood.
Database-internal transactions do not have to be compatible with any other system, so they can use any protocol and apply optimizations specific to that particular technology. For that reason, database-internal distributed transactions can often work quite well. On the other hand, transactions spanning heterogeneous technologies are a lot more challenging.
-
Exactly-once message processing
The traditional approach to synchronizing writes requires distributed transactions across heterogeneous storage systems, which I think is the wrong solution.
Transactions within a single storage or stream processing system are feasible, but when data crosses the boundary between different technologies, I believe that an asynchronous event log with idempotent writes is a much more robust and practical approach.
The big advantage of log-based integration is loose coupling between the various components.
-
XA transactions
-
Holding locks while in doubt
-
Recovering from coordinator failure
5. Fault-Tolerant Consensus
Informally, consensus means getting several nodes to agree on something. For example, if several people concurrently try to book the last seat on an airplane, or the same seat in a theater, or try to register an account with the same username, then a consensus algorithm could be used to determine which one of these mutually incompatible operations should be the winner.
The consensus problem is normally formalized as follows: one or more nodes may propose values, and the consensus algorithm decides on one of those values. In the seat-booking example, when several customers are concurrently trying to buy the last seat, each node handling a customer request may propose the ID of the customer it is serving, and the decision indicates which one of those customers got the seat.
In this formalism, a consensus algorithm must satisfy the following properties:
-
Uniform agreement
No two nodes decide differently.
-
Integrity
No node decides twice.
-
Validity
If a node decides value v, then v was proposed by some node.
-
Termination
Every node that does not crash eventually decides some value.
The uniform agreement and integrity properties define the core idea of consensus: everyone decides on the same outcome, and once you have decided, you cannot change your mind. The validity property exists mostly to rule out trivial solutions: for example, you could have an algorithm that always decides null, no matter what was proposed; this algorithm would satisfy the agreement and integrity properties, but not the validity property.
If you don’t care about fault tolerance, then satisfying the first three properties is easy: you can just hardcode one node to be the “dictator,” and let that node make all of the decisions. However, if that one node fails, then the system can no longer make any decisions. This is, in fact, what we saw in the case of two-phase commit: if the coordinator fails, in-doubt participants cannot decide whether to commit or abort.
The termination property formalizes the idea of fault tolerance. It essentially says that a consensus algorithm cannot simply sit around and do nothing forever—in other words, it must make progress. Even if some nodes fail, the other nodes must still reach a decision.
Of course, if all nodes crash and none of them are running, then it is not possible for any algorithm to decide anything. There is a limit to the number of failures that an algorithm can tolerate: in fact, it can be proved that any consensus algorithm requires at least a majority of nodes to be functioning correctly in order to assure termination.
5.1. Consensus algorithms and total order broadcast
The best-known fault-tolerant consensus algorithms are Viewstamped Replication (VSR), Paxos, Raft, and Zab. There are quite a few similarities between these algorithms, but they are not the same.
It’s sufficient to be aware of some of the high-level ideas that they have in common, unless you’re implementing a consensus system yourself (which is probably not advisable—it’s hard.
Most of these algorithms actually don’t directly use the formal model described here (proposing and deciding on a single value, while satisfying the agreement, integrity, validity, and termination properties). Instead, they decide on a sequence of values, which makes them total order broadcast algorithms.
Remember that total order broadcast requires messages to be delivered exactly once, in the same order, to all nodes. If you think about it, this is equivalent to performing several rounds of consensus: in each round, nodes propose the message that they want to send next, and then decide on the next message to be delivered in the total order.
So, total order broadcast is equivalent to repeated rounds of consensus (each consensus decision corresponding to one message delivery):
-
Due to the agreement property of consensus, all nodes decide to deliver the same messages in the same order.
-
Due to the integrity property, messages are not duplicated.
-
Due to the validity property, messages are not corrupted and not fabricated out of thin air.
-
Due to the termination property, messages are not lost.
Viewstamped Replication, Raft, and Zab implement total order broadcast directly, because that is more efficient than doing repeated rounds of one-value-at-a-time consensus. In the case of Paxos, this optimization is known as Multi-Paxos.
5.1.1. Limitations of consensus
Consensus algorithms are a huge breakthrough for distributed systems: they bring concrete safety properties (agreement, integrity, and validity) to systems where everything else is uncertain, and they nevertheless remain fault-tolerant (able to make progress as long as a majority of nodes are working and reachable). They provide total order broadcast, and therefore they can also implement linearizable atomic operations in a fault-tolerant way.
Nevertheless, they are not used everywhere, because the benefits come at a cost.
The process by which nodes vote on proposals before they are decided is a kind of synchronous replication.
Consensus systems always require a strict majority to operate. This means you need a minimum of three nodes in order to tolerate one failure (the remaining two out of three form a majority), or a minimum of five nodes to tolerate two failures (the remaining three out of five form a majority). If a network failure cuts off some nodes from the rest, only the majority portion of the network can make progress, and the rest is blocked.
Most consensus algorithms assume a fixed set of nodes that participate in voting, which means that you can’t just add or remove nodes in the cluster. Dynamic membership extensions to consensus algorithms allow the set of nodes in the cluster to change over time, but they are much less well understood than static membership algorithms.
Consensus systems generally rely on timeouts to detect failed nodes. In environments with highly variable network delays, especially geographically distributed systems, it often happens that a node falsely believes the leader to have failed due to a transient network issue. Although this error does not harm the safety properties, frequent leader elections result in terrible performance because the system can end up spending more time choosing a leader than doing any useful work.
Sometimes, consensus algorithms are particularly sensitive to network problems. For example, Raft has been shown to have unpleasant edge cases: if the entire network is working correctly except for one particular network link that is consistently unreliable, Raft can get into situations where leadership continually bounces between two nodes, or the current leader is continually forced to resign, so the system effectively never makes progress. Other consensus algorithms have similar problems, and designing algorithms that are more robust to unreliable networks is still an open research problem.
5.2. Membership and Coordination Services
Projects like ZooKeeper or etcd are often described as “distributed key-value stores” or “coordination and configuration services.” The API of such a service looks pretty much like that of a database: you can read and write the value for a given key, and iterate over keys. So if they’re basically databases, why do they go to all the effort of implementing a consensus algorithm? What makes them different from any other kind of database?
To understand this, it is helpful to briefly explore how a service like ZooKeeper is used. As an application developer, you will rarely need to use ZooKeeper directly, because it is actually not well suited as a general-purpose database. It is more likely that you will end up relying on it indirectly via some other project: for example, HBase, Hadoop YARN, OpenStack Nova, and Kafka all rely on ZooKeeper running in the background. What is it that these projects get from it?
ZooKeeper and etcd are designed to hold small amounts of data that can fit entirely in memory (although they still write to disk for durability)—so you wouldn’t want to store all of your application’s data here. That small amount of data is replicated across all the nodes using a fault-tolerant total order broadcast algorithm. As discussed previously, total order broadcast is just what you need for database replication: if each message represents a write to the database, applying the same writes in the same order keeps replicas consistent with each other.
ZooKeeper is modeled after Google’s Chubby lock service, implementing not only total order broadcast (and hence consensus), but also an interesting set of other features that turn out to be particularly useful when building distributed systems:
-
Linearizable atomic operations
Using an atomic compare-and-set operation, you can implement a lock: if several nodes concurrently try to perform the same operation, only one of them will succeed. The consensus protocol guarantees that the operation will be atomic and linearizable, even if a node fails or the network is interrupted at any point. A distributed lock is usually implemented as a lease, which has an expiry time so that it is eventually released in case the client fails.
-
Total ordering of operations
When some resource is protected by a lock or lease, you need a fencing token to prevent clients from conflicting with each other in the case of a process pause. The fencing token is some number that monotonically increases every time the lock is acquired. ZooKeeper provides this by totally ordering all operations and giving each operation a monotonically increasing transaction ID (zxid) and version number (cversion).
-
Failure detection
Clients maintain a long-lived session on ZooKeeper servers, and the client and server periodically exchange heartbeats to check that the other node is still alive. Even if the connection is temporarily interrupted, or a ZooKeeper node fails, the session remains active. However, if the heartbeats cease for a duration that is longer than the session timeout, ZooKeeper declares the session to be dead. Any locks held by a session can be configured to be automatically released when the session times out (ZooKeeper calls these ephemeral nodes).
-
Change notifications
Not only can one client read locks and values that were created by another client, but it can also watch them for changes. Thus, a client can find out when another client joins the cluster (based on the value it writes to ZooKeeper), or if another client fails (because its session times out and its ephemeral nodes disappear). By subscribing to notifications, a client avoids having to frequently poll to find out about changes.
Of these features, only the linearizable atomic operations really require consensus. However, it is the combination of these features that makes systems like ZooKeeper so useful for distributed coordination.
-
Allocating work to nodes
-
Service discovery
-
Membership services
6. References
-
Martin Kleppmann: Designing Data-Intensive Applications, O’Reilly, 2017.